sperman and pearson correlation

生信傻傻分不清的水课统计

本文回顾本科阶段学的医学统计学，概率论与数理统计，以及各种医学统计SAS，SPSS的水课系列

简单回顾定义

• Pearson 相关系数很简单，是用来衡量两个数据集的线性相关程度
• Spearman 相关系数不关心两个数据集是否线性相关，而是单调相关，Spearman 相关系数也称为等级相关或者秩相关（即rank）。

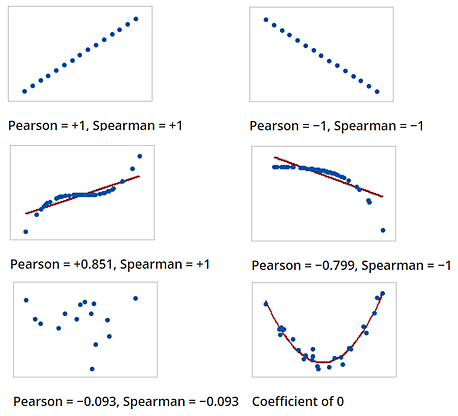
如果对 数据集 进行线性变换 比如 有 \(y=ax+b\)

Spearman和Pearson相关系数都是衡量变量之间相关性的方法，但它们有一些重要的区别：

Pearson相关系数

• 定义：Pearson相关系数是衡量两个变量之间线性相关性的指标。
• 适用范围：适用于连续型数据。
• 假设条件：
  • 数据呈正态分布（或接近正态分布）。
  • 变量之间的关系是线性的。
  • 数据点独立。
• 计算方式：通过协方差与标准差的比值来计算。
• 公式： \(\[ r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} \]\)

Spearman相关系数

• 定义：Spearman相关系数是衡量两个变量之间单调关系（不要求线性）的指标。即使关系是非线性的，只要是单调递增或单调递减的，也可以使用Spearman相关系数。
• 适用范围：适用于连续型数据和有序数据。
• 假设条件：
  • 不要求数据呈正态分布。
  • 变量之间的关系可以是任何单调关系。
  • 数据点独立。
• 计算方式：通过对数据进行排序后，再计算等级相关系数。
• 公式：$[ \rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} ]$
  • 其中，( d_i ) 是两个变量的等级差，( n ) 是样本数量。

总结

• Pearson相关系数更适合衡量线性关系，要求数据接近正态分布。
• Spearman相关系数更灵活，不要求线性关系和正态分布，更适合用于有序数据或数据非线性关系的情况。

选择使用哪种相关系数，应根据数据的性质和你要分析的具体关系类型来决定。如果你的数据可能不符合正态分布且关系可能不是线性的，Spearman相关系数通常是更好的选择。

1. 描述性统计（Descriptive Statistics）

• 均值（Mean）：数据集的平均值。
• 中位数（Median）：将数据集排序后处于中间位置的值。
• 众数（Mode）：数据集中出现频率最高的值。
• 范围（Range）：数据集中的最大值与最小值之差。
• 方差（Variance）：数据点与均值之间差异的平方的平均值。
• 标准差（Standard Deviation）：方差的平方根，表示数据点的离散程度。
• 四分位数（Quartiles）：将数据集分为四等份的三个点（Q1、Q2、Q3），Q2就是中位数。
• 偏度（Skewness）：衡量数据分布的对称性。
• 峰度（Kurtosis）：衡量数据分布的尖锐程度。

2. 推断统计（Inferential Statistics）

• 假设检验（Hypothesis Testing）：检验假设是否成立的统计方法。
  • 零假设（Null Hypothesis）：通常假设没有效果或差异。
  • 备择假设（Alternative Hypothesis）：与零假设相对立的假设。
  • p值（p-value）：用于衡量假设检验结果显著性的概率值。
• 置信区间（Confidence Interval）：估计参数值的区间范围。
• 显著性水平（Significance Level, α）：进行假设检验时的阈值，通常为0.05。

3. 回归分析（Regression Analysis）

• 线性回归（Linear Regression）：分析两个变量之间线性关系的方法。
• 多元回归（Multiple Regression）：分析多个自变量与一个因变量之间的关系。
• 非线性回归（Non-linear Regression）：分析变量之间非线性关系的方法。

4. 概率分布（Probability Distributions）

• 正态分布（Normal Distribution）：数据呈钟形曲线，均值和中位数相同。
• 二项分布（Binomial Distribution）：用于描述有两个可能结果的离散随机变量的分布。
• 泊松分布（Poisson Distribution）：用于描述一定时间内某事件发生次数的分布。
• 均匀分布（Uniform Distribution）：所有取值的概率相等。
• 指数分布（Exponential Distribution）：用于描述事件之间时间间隔的分布。

5. 采样方法（Sampling Methods）

• 简单随机抽样（Simple Random Sampling）：每个样本都有相同的被选择概率。
• 分层抽样（Stratified Sampling）：将总体分为不同的层次，然后从每个层次中随机抽样。
• 系统抽样（Systematic Sampling）：按一定规则（如每隔k个）抽取样本。
• 整群抽样（Cluster Sampling）：将总体分为多个群组，然后随机选择一些群组进行调查。

6. 非参数统计（Non-parametric Statistics）

• 曼-惠特尼U检验（Mann-Whitney U Test）：用于比较两个独立样本的非参数检验。
• 克鲁斯卡尔-沃利斯检验（Kruskal-Wallis Test）：用于比较三个或更多独立样本的非参数检验。

7. 时间序列分析（Time Series Analysis）

• 自相关（Autocorrelation）：同一时间序列在不同时间点上的值之间的相关性。
• 移动平均（Moving Average）：用于平滑时间序列数据的方法。
• ARIMA模型（Autoregressive Integrated Moving Average Model）：一种综合的时间序列预测模型。

统计学家和相关统计学概念有关的内容：

1. Karl Pearson

• Pearson相关系数：用于衡量两个变量之间线性相关性的系数。
• Pearson卡方检验（Pearson’s Chi-Square Test）：用于检验两个分类变量之间的独立性。

2. Sir Ronald A. Fisher

• Fisher’s Exact Test：用于分析两个分类变量之间的独立性，尤其适用于小样本数据。
• 方差分析（ANOVA, Analysis of Variance）：Fisher开发的用于比较多个样本均值的统计方法。
• 最大似然估计（Maximum Likelihood Estimation, MLE）：Fisher提出的一种估计参数的方法，通过最大化似然函数来找到最佳参数估计值。
• F分布（F-Distribution）：在ANOVA和回归分析中使用的一种概率分布。
• F检验（F-Test）：用于比较两个样本的方差，常用于ANOVA。

3. Francis Galton

• 回归分析（Regression Analysis）：Galton提出了最早的回归分析概念，主要用于研究遗传学中的回归现象。
• 相关（Correlation）：Galton提出了相关系数的概念，用于量化两个变量之间的关系。

4. William Sealy Gosset (笔名”Student”)

• t检验（t-Test）：Gosset提出的用于比较两个样本均值的方法，包括独立样本t检验和配对样本t检验。
• t分布（t-Distribution）：用于小样本数据的概率分布，在t检验中广泛应用。

5. Jerzy Neyman 和 Egon Pearson

• Neyman-Pearson引理（Neyman-Pearson Lemma）：提出了一种最优的假设检验方法，用于确定最佳临界区域以最大化检验的功效。
• Type I 和 Type II错误：Neyman和Pearson定义了统计检验中的两类错误：
  • Type I 错误（α错误）：拒绝了实际上为真的零假设。
  • Type II 错误（β错误）：未能拒绝实际上为假的零假设。

6. John Tukey

• 探索性数据分析（Exploratory Data Analysis, EDA）：Tukey倡导的一种通过可视化和简单统计描述来探索数据特征的方法。
• 盒须图（Boxplot）：Tukey开发的一种可视化工具，用于展示数据的分布、中心趋势和离群值。

7. David Cox

• 比例风险模型（Proportional Hazards Model）：Cox提出的一种生存分析模型，用于研究时间到事件数据。

8. Abraham Wald

• 序贯分析（Sequential Analysis）：Wald提出的用于在实验过程中进行逐步数据分析的方法，能够在中途决定是否继续实验。
• Wald检验（Wald Test）：用于检验统计模型中参数的显著性。

单变量和多变量分析

单变量分析（Univariate Analysis）

单变量分析是指对单个变量的数据进行描述和分析。这种分析主要集中在数据的集中趋势、离散程度和分布形态。

相关概念：

• 均值（Mean）：数据集的平均值。
• 中位数（Median）：排序后位于中间的值。
• 众数（Mode）：出现频率最高的值。
• 方差（Variance）：数据点与均值之间差异的平方的平均值。
• 标准差（Standard Deviation）：方差的平方根。
• 偏度（Skewness）：衡量数据分布的对称性。
• 峰度（Kurtosis）：衡量数据分布的尖锐程度。
• 范围（Range）：最大值与最小值之差。
• 百分位数（Percentiles）：将数据按百分比划分，如第25百分位数（Q1）、第50百分位数（中位数，Q2）、第75百分位数（Q3）。

重要统计学家：

• Karl Pearson：开发了许多描述性统计量，包括标准差和相关系数。

多变量分析（Multivariate Analysis）

多变量分析涉及同时分析多个变量的数据，以了解它们之间的关系和相互影响。这种分析方法广泛应用于复杂数据集和多维数据的研究。

相关概念：

• 相关分析（Correlation Analysis）：研究两个或多个变量之间的相关性。
  • Pearson相关系数（Pearson Correlation Coefficient）：衡量两个变量之间的线性相关性。
  • Spearman相关系数（Spearman Correlation Coefficient）：衡量两个变量之间的单调关系。
• 回归分析（Regression Analysis）：研究一个或多个自变量（解释变量）与因变量（响应变量）之间的关系。
  • 简单线性回归（Simple Linear Regression）：研究一个自变量与因变量之间的线性关系。
  • 多元回归（Multiple Regression）：研究多个自变量与因变量之间的关系。
• 主成分分析（PCA, Principal Component Analysis）：降维技术，通过线性变换将数据投影到低维空间。
• 因子分析（Factor Analysis）：识别数据中的潜在变量（因子），解释变量之间的相关性结构。
• 判别分析（Discriminant Analysis）：用于分类问题，根据已知类别的样本建立分类模型。
• 聚类分析（Cluster Analysis）：将数据分为若干组（簇），使得同一组内的样本相似度较高，不同组间的样本相似度较低。

重要统计学家：

• Ronald A. Fisher：开发了多元回归分析和判别分析的方法。
• Harold Hotelling：提出了主成分分析（PCA）。
• Jerzy Neyman 和 Egon Pearson：在假设检验和多变量分析中做出了重要贡献。
• John Tukey：在多变量数据分析和探索性数据分析方面做出了重要贡献。

医学统计学

1. 描述性统计（Descriptive Statistics）

• 均值（Mean）：数据集的平均值。
• 中位数（Median）：排序后位于中间的值。
• 众数（Mode）：出现频率最高的值。
• 标准差（Standard Deviation）：衡量数据的离散程度。
• 四分位数（Quartiles）：将数据集分为四等份的点，包括第25百分位数（Q1）、中位数（Q2）和第75百分位数（Q3）。

2. 假设检验（Hypothesis Testing）

• t检验（t-Test）：比较两个样本均值是否存在显著差异。
  • 独立样本t检验（Independent t-test）：比较两个独立组的均值。
  • 配对样本t检验（Paired t-test）：比较同一组在不同时间点或条件下的均值。
• 卡方检验（Chi-Square Test）：检验两个分类变量之间的独立性。
  • 卡方独立性检验（Chi-Square Test of Independence）：用于判断两个分类变量是否相关。
  • 卡方拟合优度检验（Chi-Square Goodness of Fit Test）：用于判断样本数据与预期分布是否一致。
• 方差分析（ANOVA, Analysis of Variance）：比较多个组的均值是否存在显著差异。
  • 单因素方差分析（One-way ANOVA）：比较一个因子多个水平的均值。
  • 双因素方差分析（Two-way ANOVA）：比较两个因子的多个水平的均值。

3. 相关和回归分析（Correlation and Regression Analysis）

• Pearson相关系数（Pearson Correlation Coefficient）：衡量两个连续变量之间的线性相关性。
• Spearman相关系数（Spearman Correlation Coefficient）：衡量两个变量之间的单调关系。
• 简单线性回归（Simple Linear Regression）：研究一个自变量与因变量之间的线性关系。
• 多元线性回归（Multiple Linear Regression）：研究多个自变量与因变量之间的关系。

4. 生存分析（Survival Analysis）

• 生存曲线（Survival Curve）：如Kaplan-Meier曲线，用于描述一组患者随时间的生存概率。
• 对数秩检验（Log-Rank Test）：比较两个或多个生存曲线的统计显著性。
• Cox比例风险模型（Cox Proportional Hazards Model）：用于研究多个因素对生存时间的影响。

5. 非参数检验（Non-parametric Tests）

• Mann-Whitney U检验（Mann-Whitney U Test）：用于比较两个独立样本的中位数。
• Wilcoxon符号秩检验（Wilcoxon Signed-Rank Test）：用于比较配对样本的中位数。
• Kruskal-Wallis检验（Kruskal-Wallis Test）：用于比较三个或更多独立组的中位数。

6. 诊断试验统计（Diagnostic Test Statistics）

• 灵敏度（Sensitivity）：诊断试验正确识别阳性病例的能力。
• 特异性（Specificity）：诊断试验正确识别阴性病例的能力。
• 阳性预测值（Positive Predictive Value, PPV）：阳性结果为真阳性的概率。
• 阴性预测值（Negative Predictive Value, NPV）：阴性结果为真阴性的概率。
• 受试者操作特征曲线（ROC Curve, Receiver Operating Characteristic Curve）：评估诊断试验的综合表现，通过计算曲线下面积（AUC）来衡量。

7. 临床试验设计（Clinical Trial Design）

• 随机对照试验（RCT, Randomized Controlled Trial）：将受试者随机分配到实验组和对照组，以比较干预效果。
• 盲法（Blinding）：减少偏倚的方法，包括单盲、双盲和三盲设计。
• 交叉设计（Cross-Over Design）：每个受试者在不同时间接受不同的干预，以减少个体差异的影响。

ML

机器学习领域广泛应用了许多统计学概念，以下是一些关键的统计学概念及其在机器学习中的应用：

1. 描述性统计（Descriptive Statistics）

• 均值（Mean）：用于衡量数据集的中心位置。
• 中位数（Median）：用于衡量数据集的中心趋势，特别适用于存在极值的情况。
• 标准差（Standard Deviation）：衡量数据的离散程度。
• 方差（Variance）：数据的离散程度平方，用于特征选择和评估模型性能。
• 四分位数（Quartiles）：用于衡量数据的分布情况。

2. 概率分布（Probability Distributions）

• 正态分布（Normal Distribution）：许多机器学习算法假设数据服从正态分布，如线性回归。
• 二项分布（Binomial Distribution）：用于分类问题。
• 泊松分布（Poisson Distribution）：用于事件计数模型。
• 均匀分布（Uniform Distribution）：在生成随机数时广泛使用。

3. 假设检验（Hypothesis Testing）

• t检验（t-Test）：用于比较两个样本的均值。
• 卡方检验（Chi-Square Test）：用于检验两个分类变量之间的独立性。
• p值（p-value）：用于衡量假设检验的显著性。

4. 相关和回归分析（Correlation and Regression Analysis）

• Pearson相关系数（Pearson Correlation Coefficient）：用于衡量两个变量之间的线性相关性。
• Spearman相关系数（Spearman Correlation Coefficient）：用于衡量两个变量之间的单调关系。
• 简单线性回归（Simple Linear Regression）：用于预测和关系建模。
• 多元线性回归（Multiple Linear Regression）：用于多个特征的关系建模。
• 逻辑回归（Logistic Regression）：用于二分类问题。

5. 贝叶斯统计（Bayesian Statistics）

• 贝叶斯定理（Bayes’ Theorem）：用于更新概率估计。
• 先验概率（Prior Probability）：基于先验知识的概率估计。
• 后验概率（Posterior Probability）：在观测数据后更新的概率。
• 朴素贝叶斯分类器（Naive Bayes Classifier）：一种基于贝叶斯定理的分类方法。

6. 聚类分析（Cluster Analysis）

• K均值聚类（K-Means Clustering）：一种常见的聚类算法。
• 层次聚类（Hierarchical Clustering）：构建层次结构的聚类方法。
• DBSCAN（Density-Based Spatial Clustering of Applications with Noise）：基于密度的聚类方法。

7. 降维（Dimensionality Reduction）

• 主成分分析（PCA, Principal Component Analysis）：用于数据降维和特征提取。
• 线性判别分析（LDA, Linear Discriminant Analysis）：用于分类问题中的降维。
• t-SNE（t-Distributed Stochastic Neighbor Embedding）：用于高维数据的可视化。

8. 时间序列分析（Time Series Analysis）

• 自回归模型（AR, Autoregressive Model）：用于时间序列预测。
• 移动平均模型（MA, Moving Average Model）：用于时间序列平滑。
• ARIMA模型（Autoregressive Integrated Moving Average Model）：综合的时间序列预测模型。

9. 非参数统计（Non-parametric Statistics）

• 曼-惠特尼U检验（Mann-Whitney U Test）：用于比较两个独立样本的中位数。
• 克鲁斯卡尔-沃利斯检验（Kruskal-Wallis Test）：用于比较三个或更多独立样本的中位数。

10. 评价指标（Evaluation Metrics）

• 准确率（Accuracy）：正确预测的比例。
• 精确率（Precision）：预测为正类的样本中实际为正类的比例。
• 召回率（Recall）：实际为正类的样本中被正确预测为正类的比例。
• F1得分（F1 Score）：精确率和召回率的调和平均数。
• ROC曲线（ROC Curve）：评估分类器性能的图形工具。
• AUC（Area Under Curve）：ROC曲线下的面积，用于衡量分类器的综合性能。

11. 模型选择和验证（Model Selection and Validation）

• 交叉验证（Cross-Validation）：用于评估模型性能的方法。
• 网格搜索（Grid Search）：用于超参数调优的方法。
• 贝叶斯优化（Bayesian Optimization）：用于高效的超参数调优。

这些统计学概念在机器学习中广泛应用，帮助研究人员和工程师进行数据分析、模型训练和性能评估，从而构建出有效的机器学习模型。

在机器学习中，评价指标用于评估模型的性能，以便选择最佳模型并优化其性能。不同的任务（如分类、回归、聚类等）使用不同的评价指标。以下是一些常用的评价指标：

分类任务

1. 准确率（Accuracy）
   • 定义：正确预测的样本数占总样本数的比例。
   • 公式：[ \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} ]
2. 精确率（Precision）
   • 定义：预测为正类的样本中实际为正类的比例。
   • 公式：[ \text{Precision} = \frac{TP}{TP + FP} ]
3. 召回率（Recall）
   • 定义：实际为正类的样本中被正确预测为正类的比例。
   • 公式：[ \text{Recall} = \frac{TP}{TP + FN} ]
   • 也称为灵敏度（Sensitivity）或真正率（True Positive Rate, TPR）。
4. F1得分（F1 Score）
   • 定义：精确率和召回率的调和平均数。
   • 公式：[ \text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} ]
5. 特异性（Specificity）
   • 定义：实际为负类的样本中被正确预测为负类的比例。
   • 公式：[ \text{Specificity} = \frac{TN}{TN + FP} ]
6. ROC曲线（ROC Curve, Receiver Operating Characteristic Curve）
   • 描述：绘制出不同阈值下的真正率（Recall）与假正率（False Positive Rate, FPR）的关系图。
   • AUC（Area Under Curve）：ROC曲线下的面积，用于评估分类器的综合性能。
7. 混淆矩阵（Confusion Matrix）
   • 描述：显示分类结果的矩阵，包括TP、TN、FP、FN的数量。

回归任务

1. 均方误差（MSE, Mean Squared Error）
   • 定义：预测值与实际值之差的平方的平均值。
   • 公式：[ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 ]
2. 均方根误差（RMSE, Root Mean Squared Error）
   • 定义：均方误差的平方根。
   • 公式：[ \text{RMSE} = \sqrt{\text{MSE}} ]
3. 平均绝对误差（MAE, Mean Absolute Error）
   • 定义：预测值与实际值之差的绝对值的平均值。

   • 公式：[ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n}

     y_i - \hat{y}_i

     ]

4. R²（决定系数, Coefficient of Determination）
   • 定义：衡量模型解释数据变异的程度。
   • 公式：[ R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}i)^2}{\sum{i=1}^{n} (y_i - \bar{y})^2} ]

聚类任务

1. 轮廓系数（Silhouette Score）
   • 定义：衡量聚类结果的紧密性和分离性。
   • 公式：[ s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))} ]
     • 其中 (a(i)) 是样本 (i) 到同簇内其他点的平均距离，(b(i)) 是样本 (i) 到最近的其他簇的平均距离。
2. 调整兰德指数（Adjusted Rand Index, ARI）
   • 定义：衡量聚类结果与真实标签的一致性。
   • 公式复杂，常用工具包计算。
3. 互信息（Mutual Information）
   • 定义：衡量两个分区之间的互信息量。
   • 公式复杂，常用工具包计算。

其他常用指标

1. AUC-PR（Area Under the Precision-Recall Curve）
   • 描述：PR曲线下的面积，用于评估分类器在不平衡数据集上的性能。
2. Brier Score
   • 定义：衡量概率预测的准确性，主要用于二分类问题。
   • 公式：[ \text{Brier Score} = \frac{1}{n} \sum_{i=1}^{n} (f_i - o_i)^2 ]
     • 其中 (f_i) 是预测概率，(o_i) 是实际标签（0或1）。
3. 对数损失（Log Loss, Logistic Loss）
   • 定义：衡量概率预测的损失，主要用于二分类问题。
   • 公式：[ \text{Log Loss} = -\frac{1}{n} \sum_{i=1}^{n} [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)] ]

这些评价指标帮助我们量化模型的性能，从不同角度评估其优劣，进而选择和优化最佳模型。