Traditional Feature-based Methods –Node

Meachine Learning Tasks:Review

• Node-level prediction
• Link-level prediction
• Graph-level prediction

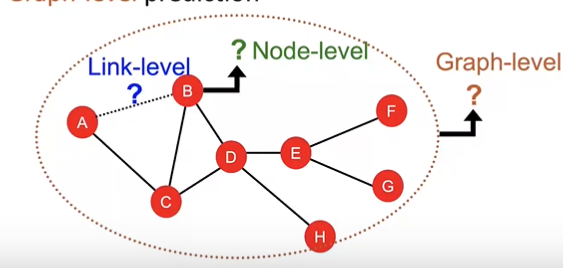
This Lecture :feature Design

Goal : Make predictions for a set of objects Design choices:

• Features:d-dimensional vectors
• Objects: Nodes,edges,sets of nodes,entire graphs
• Objective function what task are we aiming to solve

  Node-level Features:Overview

  Goal:Characterize the structure and position of a node in the network:

• Node degree
• Node centrality
• Clustering coefficient
• Graphlets

Eigenvector centrality:

Graphlets

• GDV counts graphlets
• Degree counts edges
• Clustering coefficient counts triangles

Obtain node feature:

• importance-based features:
  • Node degree
  • Different node centrality measures
• Structure-based features:
  • Node degree
  • Clustering coefficient
  • Graphlet count vector

Traditional Feature-based Methods –Link

Recap

Two formulations of the link prediction task:

• Links missing at random:
• Link over time:

Methodology

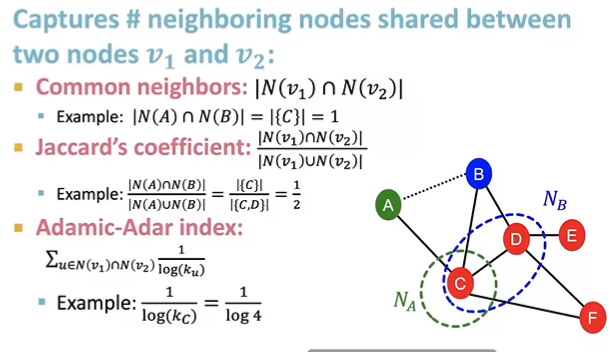
captures neighboring nodes shared between two nodes v1 and v2

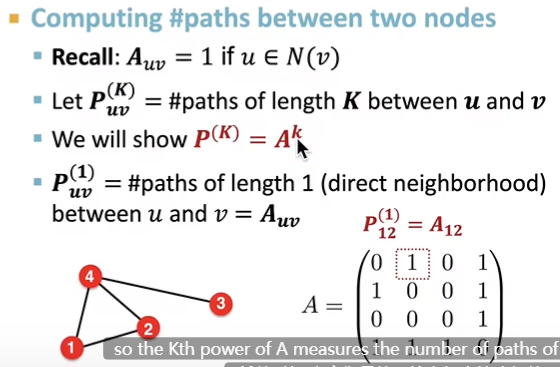
computing #paths between two nodes

Summary

• Distance-based features:
• Local neighborhood overlap
• Global neighborhood overlap

Traditional Feature-based Methods –Graph

Background:kernel Methods

Idea: Design Kernels instead of feature vectors

Graph Kernels: Measure similarity between two graphs：

• Graphlet Kernel
• Weisfeiler-Lehman Kernel
• Others
  • Random-walk kernel
  • Shortest-path graph kernel
  • etc…

Goal: Design graph feature vector Key idea: Bag-of-Words(BoW) for a graph

Both Graphlet Kernel and weisfeiler-Lehman(WL) kernel use Bag-of * representation of graph , where * is more sophisticated than node degrees!

Graphlet Features

key idea:Count the number of different graphlets in a graph.

Limitations:

Goal : design an efficient graph feature descriptor fa(G)

Idea: Use neighborhood structure to iteratively enrich node vocabulary - generalized version of Bag of node degrees

• Algorithm to achieve this: Color refinement

Color Refinement

• Given: A graph G with a set of nodes V.