CC BY 4.0 (除特别声明或转载文章外)
如果这篇博客帮助到你,可以请我喝一杯咖啡~
Exp2:基于回归分析的大学综合得分预测
本教程来源于学堂在线
一、案例简介
大学排名是一个非常重要同时也极富挑战性与争议性的问题,一所大学的综合实力涉及科研、师资、学生等方方面面。目前全球有上百家评估机构会评估大学的综合得分进行排序,而这些机构的打分也往往并不一致。在这些评分机构中,世界大学排名中心(Center for World University Rankings,缩写CWUR)以评估教育质量、校友就业、研究成果和引用,而非依赖于调查和大学所提交的数据著称,是非常有影响力的一个。
本任务中我们将根据 CWUR 所提供的世界各地知名大学各方面的排名(师资、科研等),一方面通过数据可视化的方式观察不同大学的特点,另一方面希望构建机器学习模型(线性回归)预测一所大学的综合得分。
二、作业说明
使用来自 Kaggle 的数据,构建「线性回归」模型,根据大学各项指标的排名预测综合得分。
基本要求:
- 按照 8:2 随机划分训练集测试集,用 RMSE 作为评价指标,得到测试集上线性回归模型的 RMSE 值;
- 对线性回归模型的系数进行分析。
扩展要求:
- 对数据进行观察与可视化,展示数据特点;
- 尝试其他的回归模型,对比效果;
- 尝试将离散的国家特征融入线性回归模型,并对结果进行对比。
注意事项:
- 基本输入特征有 8 个:
quality_of_education,alumni_employment,quality_of_faculty,publications,influence,citations,broad_impact,patents; - 预测目标为
score; - 可以使用 sklearn 等第三方库,不要求自己实现线性回归;
- 需要保留所有数据集生成、模型训练测试的代码;
三、数据概览
假设数据文件位于当前文件夹,我们用 pandas 读入标准 csv 格式文件的函数read_csv()将数据转换为DataFrame的形式。观察前几条数据记录:
import pandas as pd
import numpy as np
data_df = pd.read_csv('./cwurData.csv') # 读入 csv 文件为 pandas 的 DataFrame
data_df.head(3).T # 观察前几列并转置方便观察
| 0 | 1 | 2 | |
|---|---|---|---|
| world_rank | 1 | 2 | 3 |
| institution | Harvard University | Massachusetts Institute of Technology | Stanford University |
| country | USA | USA | USA |
| national_rank | 1 | 2 | 3 |
| quality_of_education | 7 | 9 | 17 |
| alumni_employment | 9 | 17 | 11 |
| quality_of_faculty | 1 | 3 | 5 |
| publications | 1 | 12 | 4 |
| influence | 1 | 4 | 2 |
| citations | 1 | 4 | 2 |
| broad_impact | NaN | NaN | NaN |
| patents | 5 | 1 | 15 |
| score | 100 | 91.67 | 89.5 |
| year | 2012 | 2012 | 2012 |
去除其中包含 NaN 的数据,保留 2000 条有效记录。
data_df = data_df.dropna() # 舍去包含 NaN 的 row
len(data_df)
2000
四、数据可视化
Top 学校
我们首先观察世界排名前十学校的平均得分情况,为此需要将同一学校不同年份的得分做一个平均。这里我们可以利用groupby()函数,将同一学校的记录整合起来并通过mean()函数取平均。之后我们按平均得分降序排序,取前十个学校作为要观察的数据。
import matplotlib.pyplot as plt # 作图
import seaborn as sns # 作图
mean_df = data_df.groupby('institution').mean() # 按学校聚合并对聚合的列取平均
top_df = mean_df.sort_values(by='score', ascending=False).head(10) # 取前十学校
sns.set()
x = top_df['score'].values # 综合得分列表
y = top_df.index.values # 学校名称列表
sns.barplot(x, y, orient='h', palette="Blues_d") # 画条形图
plt.xlim(75, 101) # 限制 x 轴范围
plt.show()
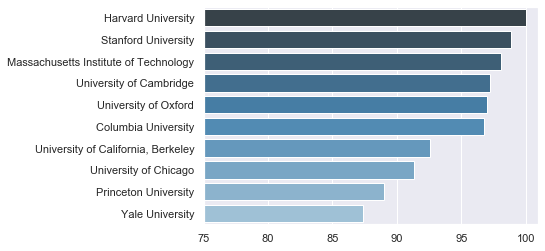
指标对比
接下来我们对比一下清北和 Top-1 的哈佛在各方面指标上差距在哪。这时雷达图非常契合我们的需求,可以直观显示出不同类别在各个指标上的差异。由于 matplotlib 和 seaborn 都没有提供官方的雷达图工具,我们通过连接 x 轴的开始和末尾自己实现一个雷达图函数(可以不关注具体细节)。
def radar_plot(dimension, Y, legend):
theta = np.linspace(0, 360, len(dimension), endpoint=False)
X_ticks = np.radians(theta)
X = np.append(X_ticks, X_ticks[0])
Y = np.hstack((Y, Y[:,0].reshape(-1, 1))) # 构建首尾相良的数据
fig, ax = plt.subplots(figsize=(9, 9), subplot_kw={'projection': 'polar'})
for i in range(Y.shape[0]):
ax.plot(X, Y[i], marker='o') # 画图
ax.set_xticks(X)
ax.set_xticklabels(dimension, fontsize='large')
ax.set_yticklabels(np.linspace(-np.min(Y), 0, 6).astype(int))
ax.spines['polar'].set_visible(False) # 不显示成环的 x 轴
ax.grid(axis='y')
n_grids = np.linspace(np.min(Y), 0, 6, endpoint=True) # grid 的网格数
grids = [[i] * (len(X)) for i in n_grids] # grid 的半径
for i, grid in enumerate(grids[:-1]): # 给 grid 填充间隔色
ax.plot(X, grid, color='grey', linewidth=0.5)
if i > 0 and i % 2 == 0:
ax.fill_between(X, grids[i], grids[i-1], color='grey', alpha=0.1)
plt.legend(legend, fontsize='small')
plt.show()
china_df = mean_df.loc[['Tsinghua University', 'Peking University']]
contrast_df = pd.concat([top_df.head(1), china_df]) # 构建对比数据
feature_cols = ['quality_of_faculty', 'publications', 'citations', 'alumni_employment',
'influence', 'quality_of_education', 'broad_impact', 'patents']
contrast_df = contrast_df[feature_cols] # 取出指标对应的列
sns.set_style('white')
radar_plot(feature_cols, -contrast_df.values, contrast_df.index) # 画雷达图
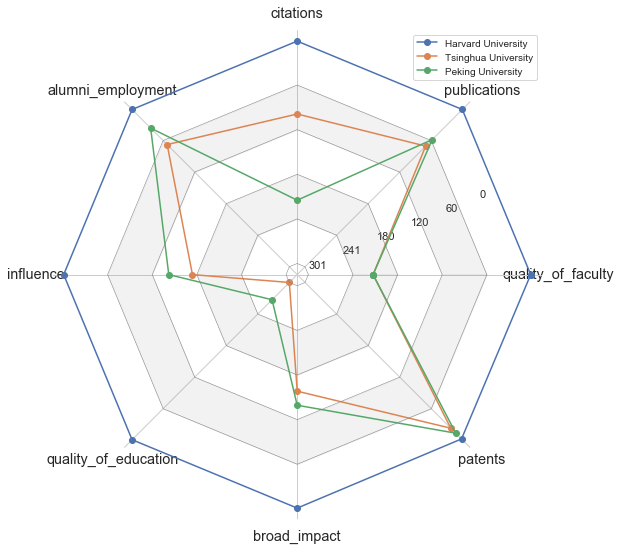
可以看到哈佛大学在各项指标上一骑绝尘,清北虽然在论文发表、专利和就业率上排名较高,但在师资和教育质量上差距较大,同时影响力方面处于中等水平。清北内部来看,清华在引用量上显著优于北大,而在其他方面相比北大稍弱一些。
五、模型构建
取出对应自变量以及因变量的列,之后就可以基于此切分训练集和测试集,并进行模型构建与分析。
feature_cols = ['quality_of_faculty', 'publications', 'citations', 'alumni_employment',
'influence', 'quality_of_education', 'broad_impact', 'patents']
X = data_df[feature_cols]
Y = data_df['score']
X
| quality_of_faculty | publications | citations | alumni_employment | influence | quality_of_education | broad_impact | patents | |
|---|---|---|---|---|---|---|---|---|
| 200 | 1 | 1 | 1 | 1 | 1 | 1 | 1.0 | 2 |
| 201 | 4 | 5 | 3 | 2 | 3 | 11 | 4.0 | 6 |
| 202 | 2 | 15 | 2 | 11 | 2 | 3 | 2.0 | 1 |
| 203 | 5 | 10 | 12 | 10 | 9 | 2 | 13.0 | 48 |
| 204 | 10 | 11 | 11 | 12 | 12 | 7 | 12.0 | 16 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2195 | 218 | 926 | 812 | 567 | 845 | 367 | 969.0 | 816 |
| 2196 | 218 | 997 | 645 | 566 | 908 | 236 | 981.0 | 871 |
| 2197 | 218 | 830 | 812 | 549 | 823 | 367 | 975.0 | 824 |
| 2198 | 218 | 886 | 812 | 567 | 974 | 367 | 975.0 | 651 |
| 2199 | 218 | 861 | 812 | 567 | 991 | 367 | 981.0 | 547 |
2000 rows × 8 columns
all_y = data_df['score'].values
all_x = data_df[feature_cols].values
# 取 values 是为了从 pandas 的 Series 转成 numpy 的 array
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(all_x, all_y, test_size=0.2, random_state=2020)
all_y.shape, all_x.shape, x_train.shape, x_test.shape, y_train.shape, y_test.shape # 输出数据行列信息
((2000,), (2000, 8), (1600, 8), (400, 8), (1600,), (400,))
from sklearn.linear_model import LinearRegression
LR = LinearRegression() # 线性回归模型
LR.fit(x_train, y_train) # 在训练集上训练
p_test = LR.predict(x_test) # 在测试集上预测,获得预测值
test_error = p_test - y_test # 预测误差
test_rmse = (test_error**2).mean()**0.5 # 计算 RMSE
'rmse: {:.4}'.format(test_rmse)
'rmse: 3.999'
得到测试集的 RMSE 为 3.999,在百分制的预测目标下算一个尚可的结果。从评价指标上看貌似我们能根据各方面排名较好的预估综合得分,接下来我们观察一下学习到的参数,即各指标排名对综合得分的影响权重。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
sns.barplot(x=LR.coef_, y=feature_cols)
plt.show()
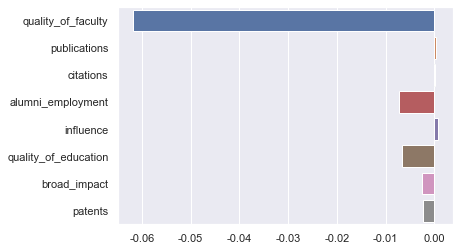
这里会发现综合得分的预测基本被「师资质量」这一自变量主导了,「就业」和「教育质量」这两个因素也有一定影响,其他指标起的作用就很小了。
为了观察「师资质量」这一主导因素与综合得分的关系,我们可以通过 seaborn 中的regplot()函数以散点图的方式画出其分布。
sns.regplot(data_df['quality_of_faculty'], data_df['score'], marker="+")
plt.show()
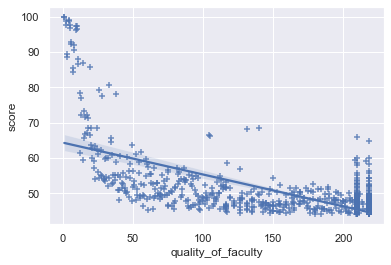
可以看到师资质量和得分确实有一定的负相关关系,但明显并不是线性的,因此用排名做线性回归只能得到尚可的结果。
六、讨论
- 对特征做变换
- 输入取 log
- 输出能不能取 log?
- 双重 log?
- 多项式特征:PolynomialFeatures
- 输入取 log
- 输入特征间的共线性
broad_impact?- one-hot 形式引入离散的国家特征?
- 岭回归、Lasso 回归
- 显著性检验
- 不同方法间 pair t-test
- 线性回归系数
